Polarization#
To understand how an optical waveguide works, it is important to understand what it means for light to be polarized. The polarization of light affects how it behaves in a waveguide.
The diagram below describes the motion of a wave of light, which is an electromagnetic wave:
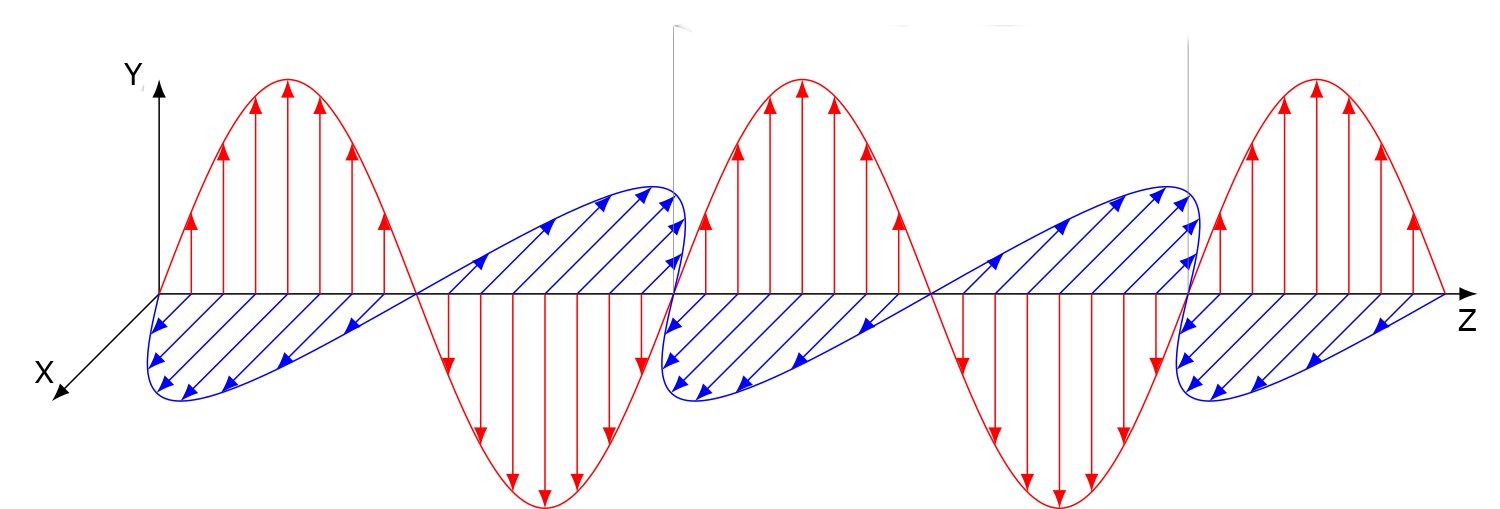 []
[]
As the light wave propagates in the positive z direction, electric and magnetic field components of the light wave propagate in the x direction and y direction. The electric and magnetic field components propagate orthogonally to one another, and orthogonal to the light wave’s direction of propagation.
The polarization of a light wave generally refers to the orientation of its electric field vector. Why do we care about the electric field vector and not the magnetic field vector? This is purely convention. Because the electric and magnetic fields are orthogonal to one another, knowing the orientation of a light wave’s electric field and its direction of propagation tells us all we need to know about the orientation of its magnetic field too.
If the electric field of a light wave is orthogonal to the interface through which the light wave propagates, the light wave has perpendicular polarization. These light waves are also known as transverse electric (TE) waves. On the other hand, if the electric field of a light wave is parallel to the interface of propagation, it has parallel polarization. These waves are also called transverse magnetic (TM) waves.
Polarization conventions can be a bit tricky to understand at first. Let’s take a look at the diagram above for a better understanding. A light wave propagates in the z direction, while electric and magnetic fields propagate in the x direction and the y direction. The red and blue field lines could represent either the electric field or the magnetic field respectively. This is a three dimensional graph, but what if we considered it in only two dimensions? Let’s take the y-z plane, the slice of the graph where x=0. If we were to look at this plane straight on, we’d only see the red field lines oscillating along the y axis and the arrow in the positive z direction representing the direction of propagation. The red field lines are parallel to the y-z plane, the blue field lines are orthogonal to (transverse) the y-z plane.
Note
Test your comprehension of TE and TM polarization:
What is the polarization of the light wave in the diagram if the red field lines represent the electric field and the blue field lines represent the magnetic field?
What is the polarization of the light wave in the diagram if the red bield lines represent the magnetic field and the blue field lines represent the electric field?
Polarization: Considerations#
Natural light (say, the light from the sun) is unpolarized (well, mostly–when it scatters from molecules in the atmosphere sunlight becomes partially polarized). That’s not to say that the light doesn’t have electric and magnetic field components, all light does, but the orientation of the electric and magnetic field components is scattered and non-uniform. It’s possible to polarize unpolarized light by filtering out light with certain polarizations and permitting light with other polarizations. Once light is polarized, it’s a lot more useful for transmitting data. Polarized light behaves predictably, unpolarized light behaves unpredictably.
The behavior of light in a waveguide depends in part on its polarization, which we’ll explore in the next section. Some waveguides support light of certain polarizations and not others in certain modes, and most waveguides can support multiple photonic signals of different polarizations simultaneously.


